Seit der Entwicklung der ersten selbstfahrenden Schienenfahrzeuge zu Beginn des 19. Jahrhunderts bis zum heutigen Tag hat sich die Grundanforderung an die Kraftübertragung zwischen den Antriebsaggregaten und den Triebrädern nicht verändert:
Die mechanische Antriebsenergie muss vom starr im Rahmen gelagerten Motor/Dampfzylinder auf die vertikal gefederte Antriebsachse übertragen werden, ohne dabei deren Federcharakteristik zu beeinflussen.
Unabhängig der gewählten Kraftübertragungsart stellt sih dabei immer dieselbe Problematik:
Federn Triebachsen in vertikaler Richtung ein, so ändern sich die Abstände zwischen den Achsen, als auch zu den Antriebsaggregaten.
Diese Längenunterschiede müssen von der Mechanik - sei es durch Treib- und Kuppelstangen oder durch Zahnradgetriebe - ausgeglichen werden können.
Die für die Kraftübertragung erforderliche Mechanik hat möglichst einfach auszufallen, denn jede unnötige rotierende oder oszillierende Masse erzeugt Beschleunigungs- oder Fliehkräfte, welche mit zunehmender Fahrgeschwindigkeit grösser werden und somit die maximale Fahrgeschwindigkeit der «Stangenlokomotiven» beschränken. Und jede zusätzliche Zahnradpaarung bringt wegen der Lager- und Zahnflankenreibung eine Einbusse im Wirkungsgrad von 4 bis 6 % mit sich, was bei den hohen übertragenen Leistungen bei Lokomotiven entsprechend ins Gewicht fällt.
Vor der Entwicklung von leistungsfähigen Elektromotoren in kleiner Baugrösse gab es zum Stangenantrieb keine wirkliche Alternative:
Dampflokomotiven waren im selben Masse auf Treibstangen angewiesen, wie Otto-Motoren auf die «Pleuel», um die lineare Kolbenbewegung in eine kontinuierliche Kreisbewegung umzuwandeln.
Zudem waren während den Anfängen der Elektrotraktion die Dimensionen leistungsfähiger Elektromotoren so gewaltig, dass an einen Einzelachsantrieb aus Platz- und Gewichtsgründen nicht zu denken war: Wegen des grossen Motorendurchmessers rückte ein allfälliges Ritzel zur Antriebsachse in weite Ferne und das Gewicht der erforderlichen elektromechanischen Apparate wäre pro Achse wesentlich grösser ausgefallen, als dies der maximal erlaubte Achsdruck zugelassen hätte. So blieb den Konstrukteuren des frühen 20. Jahrhunderts nichts anderes übrig, als auf den Einzelachsantrieb zu verzichten und wenige Motoren mit mehreren Triebachsen zu Antriebseinheiten zusammen zu fassen. Dies geschah am einfachsten und wirtschaftlichsten mit Hilfe von Treib- und Kuppelstangen und allenfalls noch einem einstufigen Zahnradgetriebe als Drehmomentwandler.
Das Drehmoment M, das von einer Stange übertragen werden kann, ist das Produkt aus der Druck- oder Zugkraft F und dem vertikalen Abstand vom Triebzapfen- zum Triebachszentrum a:
Je nach Position des Gestänges ist der Vertikalabstand a zum Triebachszentrum unterschiedlich gross:
Gemäss obenstehender Betrachtung durchläuft eine Kuppelstange pro Radumdrehung jeweils neben zwei optimalen Arbeitspunkten (90°/270°) auch zwei «tote Punkte» (M = 0 N/m) (0°/180°). Eine Stangenlokomotive, welche mit all ihren Stangen im «toten Punkt» zum Stillstand gekommen wäre, könnte ohne fremde Hilfe nicht wieder anfahren, da sie kein Drehmoment mehr vom Fahrmotor auf die Räder übertragen kann. Aus diesem Grunde laufen die Treibstangen bei allen Stangenlokomotiven nicht synchron oder spiegelverkehrt, sondern sind um 90° versetzt. Wenn sich nun das Gestänge auf einer Seite der Lok am «toten Punkt» befindet, arbeitet es auf der anderen Seite am optimalen Arbeitspunkt. Man kann beim Gestänge einer Lokomotive nicht von einer Arbeitsaufteilung reden. Vielmehr ergänzen sich die linke und die rechte Seite einer Lok. Jede Seite muss also in der Lage sein, die volle Leistung einer Antriebseinheit zu übernehmen.
Eine Regel besagt, dass das Gestänge auf der in Fahrtrichtung rechten Seite dem Linken um 90° voraus eilt. Diese Regel ist aber nicht physikalisch, sondern herstellungstechnisch begründet.
Die zu übertragenden Drehmomentanteile wurden im graphisch dargestellten Beispiel als Sinuskurven definiert, was der Realität auch am nächsten kommen dürfte.
Schliesslich sind die einzigen exakt bestimmbaren Werte die vier Schnittpunkt der beiden Kurven jeweils bei 50 %.
Die übrigen Punkte variieren mit der Elastizität des Gestänges und des Lokomotivrahmens, sowie der Lagerspielaufteilung.
Zudem muss die Summe der beiden Drehmomentanteile des linken und des rechten Gestänges 100 % ergeben.
Anhand der beiden Drehmomentanteile konnten die Belastungskurven der Kuppelstangen in Prozent errechnet werden, wobei 100 % der Belastung einer Stange am optimalen Arbeitspunkt bei 90° und 270° entspricht.
Beim Betrachten der Graphik fällt auf, dass bei einem Winkel α von 45° (45°, 135°, 225° und 315°) die Kuppelstangenbelastung 70,7 % beträgt (sin45° = 0.707).
Trotz konstantem Drehmoment über die volle Radumdrehung beträgt die Summe beider Kuppelstangenbelastungen an diesen vier Positionen 141 % derjenigen einer Kuppelstange am optimalen Arbeitspunkt.
Da das übertragene Drehmoment konstant ist, würde der Motor von diesem Anschwellen der Summenkräfte im Gestänge nichts zu spüren bekommen, wären da nicht die Reibungsverluste in den Stangenlagern.
Diese ändern sich stets proportional zur Lagerbelastung. An den optimalen Arbeitspunkten des Gestänges beträgt somit die zu überwindende Lagerreibung lediglich ²/3 von derjenigen bei 45°.
Je nach Stangenanordnung und mechanischem Zustand der Lokomotive fallen die übrigen pulsierenden Reibungswiderstände - welche mehrere Prozent der abgegebenen Motorenleistung betragen - ab etwa der ausgefahrenen Stundenleistung der Lokomotive bei langsamen Geschwindigkeiten spürbar ins Gewicht.
Daraus erfolgt eine unruhige Laufkultur, welche oft fälschlicherweise als Klemmen des Gestänges oder als Unwucht interpretiert wird.
Stangenlokomotiven belastete seit jeher ein bereits angesprochenes Problem:
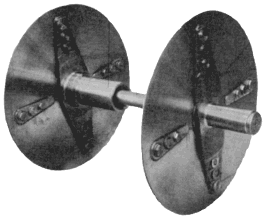
Die rotierende, exzentrisch angeordnete Masse der Treib- und Kuppelstangen erzeugt Zentrifugalkräfte, die mit Gegengewichten bestmöglichst ausgewuchtet werden müssen.
Unwucht bedeutet nichts anderes als das Verschieben des Massenschwerpunktes aus dem Rotationszentrum. Diese Exzentrizität des Massenschwerpunktes gewinnt mit zunehmender Geschwindigkeit an
Kräftemässigem Einfluss, was sich in Abhängigkeit der Konstruktionsart in mehr oder weniger heftigen Nickbewegungen in der gesamten Lokomotive und sogar in den angehängten Wagen bemerkbar macht.
Der Gesamtmasseanteil der Kuppelstange und des Kurbelzapfens m1 [kg] bewegt sich auf dem Radius r1 [m] um das Radachs- bezw. Rotationszentrum Z.
Die Masse des Ausgleichsgewichtes m2 bewegt sich in unmittelbarer spurkranznähe auf dem Radius r2 und bewirkt die für den dynamischen Kräfteausgleich zur Zentrifugalkraft F1 erforderliche Reaktionskraft F2.
Während die Masse des zu tragenden Gestänges m1 und die Radien r1 und r2 aufgrund z.B. des Kolbenhubes (bei Kolbendampfmaschinen) und des Triebraddurchmessers gegeben sind, lässt sich die Masse des erforderlichen Gegengewichtes statisch mit Hilfe des Hebelgesetztes berechnen:
Im folgenden Beispiel sollen die Zentrifugalkraft und die Reaktionskraft der bayrischen S 2/6 über den gesamten Geschwindigkeitsbereich errechnet und verglichen werden.
Betrachtet wird die Triebachse Nr. 2 (einseitig mit einer Kuppelstange verbunden, ohne Treibstange).
Für die grobe Berechnung werden folgende Werte angenommen: m1 = 100 kg (inkl. Kurbelzapfen und Exzentergussmasse des Speichenrades), r1 = 325 mm und r2 = 1000 mm.
Daraus ergibt sich für das Ausgleichsgewicht m2 = 65 kg.
Zentrifugalkräfte werden mit folgender Formel ermittelt:
Als zusätzlicher Parameter ist der Drehzahlbereich zu definieren:
0-360 1/min (entspricht 0-150 km/h).
Daraus ergibt sich folgende Tabelle:
| v [km/h] |
n [1/min] |
F1 [kN] |
F2 [kN] |
F1/2 entspricht der Gewichtskraft folgender Massen in Tonnen |
| 0 | 0 | 0 | 0 | 0 |
| 37 | 90 | 2.886 | 2.886 | 0.294 |
| 75 | 180 | 11.547 | 11.547 | 1.177 |
| 107 | 270 | 25.981 | 25.981 | 2.648 |
| 150 | 360 | 46.189 | 46.189 | 4.708 |
Aus der obenstehenden Tabelle lässt sich erkennen, dass die Fliehkräfte der Kuppelstange F1 und des Ausgleichsgewichtes F2 über den gesamten Geschwindigkeitsbereich identisch sind und sich somit stets ausgleichen. Es wird aber auch deutlich, dass die Einzelnen Fliehkräfte mit zunehmender Geschwindigkeit nicht proportional, sondern progressiv zunehmen: So beträgt die Differenz zwischen 0 und 90 1/min lediglich ca. 3 kN während die Differenz zwischen 270 und 360 1/min bereits mit ca. 20 kN beziffert werden muss.
Mit Ausnahme von modernen Hochgeschwindigkeitszügen kommen im Eisenbahnbau vorwiegend Räder zum Einsatz, welche im Sandguss- oder Schmiedeverfahren hergestellt wurden.
Diese Herstellungsarten bringen gegenüber der Spanabhebenden Fertigung grössere Herstellungstoleranzen mit sich.
Ungenauigkeiten im Mass und in der Geometrie bedeuten immer eine Verschiebung des Massenschwerpunktes und somit eine Unwucht.
Diese Unwucht kann man sich auch als «dritte Masse» m3 vorstellen, welche sich in ihrem Wirken nicht von den Massen m1 und m2 unterscheidet:
Mit zunehmender Drehzahl erzeugt sie eine Fliehkraft F3, welche nun aber nicht von einem Gegengewicht ausgeglichen wird!
Folgendes Diagramm zeigt das Wirken eines Triebrades der S 2/6 in voller Fahrt bei einem angenommenen Radgewicht von 1000 kg und einer Massenschwerpunktverschiebung von lediglich 1 cm:
Bei 150 km/h würde unter diesen Umständen eine Fliehkraft von über 14 kN entstehen, was der Gewichtskraft einer Masse von ca. 1.4 Tonnen entspricht.
Bei den beschriebenen Berechnungen stand nicht das Ermitteln von exakten Werten im Vordergrund. Vielmehr ging es darum, mit ungefähr geschätzten Ausgangsparametern auf einfache Art und Weise einen Eindruck über die Kräfteentwicklung in einem Triebrad einer «Stangenlokomotive» zu vermitteln. So lässt sich auch die Leistung der damaligen Konstrukteure und Handwerkern besser würdigen, welche Räder, Stangen und die Beschleunigungskräfte von Kolben, Kolbenstangen und Treibstangen zu berechnen und auszuwuchten hatten, so, dass auch im hohen Geschwindigkeitsbereich noch eine annehmbare Laufkultur des Fahrzeuges bestand.
Zusätzlich zur Komforteinbusse wirken die Zentrifugalkräfte zerstörerisch auf die Treib- und Kuppelstangen selber ein, da sie - ausgerechnet zu jenem Zeitpunkt, wo die zu übertragenden Drehmomente am optimalen Arbeitspunkt am grössten sind - ein starkes Biegemoment hervorrufen.
Die effektive Belastung der Treib- und Kuppelstangen setzt sich aus Zug- bzw. Druckspannungen und Biegespannungen zusammen, wobei letztere bei steigender Drehzahl eine zunehmend dominante Rolle spielen.
Da mit wachsender Fahrgeschwindigkeit die Stangen einer entsprechend grösseren Belastung ausgesetzt sind, muss die Geschwindigkeit einer Stangenlokomotive begrenzt werden, um ein Zerstören des Gestänges zu verhindern.
Für die folgende Betrachtung wird die Zug- / Druck- und Biegebeanspruchung der Kuppelstange zwischen den Achsen 1 und 2 (5 und 6) der Be 6/8''' der SBB untersucht. Die auch unter dem Namen «Krokodil» bekannte Lokomotive ist die leistungsfähigste Einheit der Schweiz, die mit einem Winterthurer Schrägstangenantrieb ausgerüstet worden ist. Charakteristisch für diesen Stangenantrieb sind die mit langen Kuppel- und Treibstangen zu überwindenden grossen Distanzen über zwei Wellenabstände.
Aufgrund der Baulänge von 3 m ist das Kuppelstangengewicht auf über 100 kg angestiegen.
Bei 75 km/h Spitzengeschwindigkeit (295 1/min) entwickelt diese rotierende Masse eine Zentrifugalkraft von mehr als 30 kN (3 t).
Um die statischen Gegebenheiten der Treibstange zu bestimmen, sind drei Faktoren von Interesse:
Die Be 6/8''' entwickelt beim Anfahren eine Zugkraft von 300 kN. Um die erforderlichen 50 kN auf das Triebrad zu übertragen, wird die beschriebene Kuppelstange am optimalen Arbeitspunkt mit 112.5 kN (11.25 t) belastet. Der grossen Querschnittsfläche verdankt die mächtige Stange eine günstige Zug- und Druckspannung von lediglich 24.5 N/mm²: Dies entspricht etwa 1/7 des zulässigen Wertes eines handelsüblichen Baustahles (St 37) bei Wechselbelastung.
Mit einem Schlankheitsgrad der Kuppelstange von weniger als 90 kann von einer unelastischen Knickbeanspruchung (Tetmajerfall) ausgegangen werden. Die Knicksicherheit ist aber in jedem Fall mit einem Mindestfaktor von 10 bis 11 zweifelsfrei gegeben. Gemäss den allgemeinen Richtlinien von 1914 sind Faktoren von 6 bis 8 vorgeschrieben.
Die stärkste Belastung erfährt die Kuppelstange durch die bereits erwähnte Zentrifugalkraft:
Diese bewirkt in der Mitte der Stange ein Biegemoment von bis zu 11800 Nm, bzw. in den Randfasern des Materiales eine Biegespannung von bis zu 112 N/mm².
D.h. der Belastungsanteil der Kuppelstange durch die Biegung ist in den Randfasern etwa viermal grösser als derjenige durch Druck- oder Zugkraft.
Das Biegemoment zwingt die Kuppelstange zu einer Durchbiegung von ca. 10 mm.
Die Graphik stellt die max. Biegemomente und Biegespannungen über die gesamte Länge der Kuppelstange, sowie die Biegemomente und -spannungen in der am stärksten belasteten Stangenmitte in Abhängigkeit der Fahrgeschwindigkeit dar.
Im Gegensatz zu allen anderen genau berechneten Kurven ist die scheinbare Konstante für die max. Druck- oder Zugspannung stark abstahiert.
In der Realität erreicht die Lokomotive - in Abhängigkeit der Drehmomentkurve des Motors - diesen Wert lediglich bei etwa 35 km/h.
Anschliessend sinkt sie mit zunehmender Geschwindigkeit auf etwa 50% bis 30% ab.
Die Priorität wurde aber nicht auf die exakte Darstellung dieser Kurve gelegt, sonder auf die Feststellung, dass bei dieser Kuppelstange die maximale durch die Mororenleistung erreichte Zug- uder Druckspannung nur etwa ¼ der durch die Zentrifugalkraft hervorgerufenen Materialbelastung entspricht.
Bei Dampflokomotiven ist der Exzenterradius der Kurbelzapfen r1 durch den Kolbenhub im Dampfzylinder in einem für die Dampfenergienutzung sinnvollen Rahmen gegeben.
Aber auch bei elektrischen «Stangenlokomotiven» wurde dieser Radius in vergleichbaren Dimensionen möglichst klein gehalten, um die Umfangsgeschwindigkeit und somit die Zentrifugalkräfte der Treib- und Kuppelstangen möglichst gering zu halten.
Diese Massnahme erhöht zwar wegen der kleineren «Hebellänge» in jeder Stange die Zug- und Druckspannung, reduzierte aber in weit grösserem Masse die Gesamtbelastung durch eine wesentlich geringere Biegebeanspruchungsanteil.
Die Dimensionierung des Exzenterradius r1 liegt oft im Bereich zwischen 275 - 325 mm.
Die angewandte maximale Drehzahl nmax pendelte sich in Abhängigkeit der zur Verfügung stehenden Metallurgie und der Schmierart der Stangenlager auf etwa 250 bis 350 1/min ein.
Je nach gewünschter Maximalgeschwindigkeit vmax und Zugkraft wird beim Stangenantrieb sozusagen als einzige Variable jeweils der Triebraddurchmesser angepasst, wobei das gewählte Mass immer als Kompromis zu verstehen war:
Güterzugs- oder Gebirgslokomotiven, welche prioritär hohe Zugkräfte zu entwickeln hatten, wurden mit wesentlich kleineren Triebrädern ausgerüstet als Schnellzugslokomotiven mit hohen Spitzengeschwindigkeiten für Einsätze im Flachland.
Schnelle Universallokomotiven mit hohen Zugkräften - wie man sie seit Mitte des 20. Jahrhunderts kennt - waren im «Stangenzeitalter» undenkbar.
| Loktyp | vmax [km/h] | øTriebrad [mm] | nmax [1/min] |
| C 5/6: SBB, 1913 | 65 | ca. 1350 | 255 |
| A 3/5: SBB, 1902 | 90 | ca. 1800 | 265 |
| Ce 6/8''/Be 6/8'': SBB 1920 | 65/75 | 1350 | 255/295 |
| Ae 3/6'': SBB 1924 | 100 | 1610 | 330 |
| Be 5/7/Ae 5/7: BLS | 75/90 | 1350 | 294/354 |
| S 2/6: K.BAY.STS.B. 1906 | 150 | 2200 | 362 |
| BR 05: DR 1934 | 175 (200) | 2300 | 404 (461) |
| Class S-1 6100: PR 1938 | 192 (227) | 2134 | 477 (564) |
Tabelle mit verschiedenen Lokomotivtypen, deren maximalen Fahrgeschwindigkeiten und Triebraddrehzahlen
Die obere Drehzahlgrenze von ca. 350 1/min wurde nur von wenigen Lokomotiven und vorwiegend auf Rekordfahrten und nicht im Dauerbetrieb überschritten. Während die Baureihe 05 der deutschen Reichsbahn 1934 bereits von einer weit fortgeschrittenen Metallurgie und Schmiertechnik profitierte, wurden bereits Ende des 19. Jahrhunderts vor allem von der deutschen Lokomotivindustrie im Fahrzeugbau Konstruktionstechniken angewandt, denen man sich - abgesehen von statischen Fachwerkkonstruktionen wie Brücken - erst zur Zeit des Zweiten Weltkrieges vorwiegend im Flugzeugbau wieder bediente.
So wurden z.B. die Querschnitte der beweglichen Teile dem jeweiligen Belastungsverlauf der Biegespannung angepasst.
Nach diesen Kriterien gefertigte Kuppelstangen sind in deren Mitte am mächtigsten ausgebildet und verjüngen sich mit abnehmender Distanz zu den Stangenlagern.
Mit Hilfe der durch die Verjüngung erreichte Gewichtseinsparung wurden im Betrieb die Fliehkräfte reduziert.
Entsprechend konnte die Stangenbelastung durch Fliehkräfte bei gleicher Drehzahl verringert, und die maximale Drehzahl entsprechend erhöht werden.
Noch in den achzigerjahren des 19. Jahrhunderts wurden für die Dimensionierungen diese Bombierungen lediglich Empfehlungen ausgesprochen, wonach das Gestänge in der Mitte um 10% bis 30% mächtiger auszubilden wäre.
Dabei überliess man es dem Gefühl des jeweiligen Konstrukteurs, in welchem Bereich von diesem für Ingenieure schon fast gigantischen Spielraum er seine Konstruktion ansiedeln wollte.
Erst zu Beginn des 20. Jahrhunderts begann man aufgrund der zu erwartenden Stangenbelastung die Wiederstandsmomente für verschiedene Positionen rechnerisch zu ermitteln und den jeweiligen Stangenquerschnitt nach mathematischen Kriterien exakt anzupassen. 1906 erreichte diese Entwicklung mit der bayrischen S 2/6 aus dem Hause Maffay einen ersten Höhepunkt, welche mit einem gewichtsoptimierten Fahrwerk und einem Triebraddurchmesser von 2200 mm eine für die damalige Zeit sensationelle Maximalgeschwindigkeit von 154.4 km/h in der Horizontalen erreichte.
Den Historiker müsste die Tatsache eigentlich erstaunen, dass solche gewichtsoptimierten Konstruktionen, wie sie 1906 von Maffay mit grossem Erfolg angewendet wurden, in nachfolgenden Entwicklungen nicht mehr oder nur sehr selten integriert worden sind. Da bereits 1910 entsprechende Vorschläge formuliert worden sind, wonach Kuppelstangen zu den Lagerköpfen hin kontinuierlich ca. 20% zu verjüngen seien, ist nicht anzunehmen, dass die Belastungsanteile von Druck- und Zugspannungen sowie Biegespannungen falsch Bewertet wurden. Eher dürfte das stark verteuerte Herstellungsverfahren eine Rolle gespielt haben. Leider gibt es aber innerhalb eines Stangenantriebssystems auch Faktoren, die schwer oder gar nicht berechnenbar sind. Aufgrund dieses Unsicherheitsfaktores zögerten die Konsrukteure zum Teil auch zurecht mit einem gewichtsoptimierteren Materialeinsatz.
Im Gegensatz zur Kohle, welche importiert werden musste, war die zur Gewinnung von elektrischer Energie benötigte Wasserkraft in der Schweiz in genügendem Masse vorhanden.
Im Interesse einer energiepolitischen Unabhängigkeit versuchten die Schweizer Bahnen schon früh, das Potential der Elektrizität zur Traktionsförderung auszunutzen.
So wurde bereits im ersten Jahrzeht des zwanzigsten Jahrhunderts auf verschiedenen Versuchsstrecken erste Erfahrungen mit dem elektrischen Betrieb von Eisenbahnen gesammelt.
Der Ausbruch des ersten Weltkrieges und die damit verbundene Kohleknappheit in der Schweiz zwang die Bahnunternehmungen, die Einführung der elektrischen Traktionsmittel dramatisch zu beschleunigen.
Obwohl für die ersten elektrischen Versuchslokomotiven, welche von den SBB 1917 bestellt und 1919 zur Ablieferung gelangten, immer noch der von den Dampflokomotiven bewährte Stangenantrieb vorgesehen war, erkannten die Konstrukteure, dass ein Einzelachsantrieb gegenüber dem Stangenantrieb wesentlich höhere Geschwindigkeiten zulassen würde.
Parallel zum Bau der eigentlichen Versuchslokomotiven, wurde die Enwicklung von Einzelachsantrieben vorangetrieben.
Der Einzelachsantrieb verfügt aber gegenüber dem Kuppeln von mehreren Triebachsen nicht nur Vorteile: Vor allem wegen der Neigung zum Schleudern (Durchdrehen der Räder bei vorwiegend schlechten Schienenverhältnissen) einzelner Triebachsen übten Skeptiker des Einzelachsantriebes berechtigte Kritik. Nachdem die mechanischen Probleme der Kraftübertragung vom Fahrmotor auf die Triebachsen gelöst waren, sollte es schliesslich auch noch mehr als ein halbes Jahrhundert dauern, bis die Steuerungstechnik brauchbare Lösungsansätze als Kompromiss zu dieser Problematik lieferte. (Mehr zum Thema «Schleuderschutz» unter «Steuerungstechnik».)
Bei Antriebssystemen, welche ohne elastische Elemente arbeiten, wird die Kraftübertragung wie beim Stangenantrieb mit starren Stangen, Hebeln, Zahnrädern, Kardanwellen, Kulissen und Kulissensteinen bewältigt.
Drehmomentschwankungen werden ungedämpft vom Ritzel auf die Triebachse und umgekehrt übertragen, da keine Federelemente wie Spiralfedern und Torsionsstangen für deren Dämpfung und den federwegbedingten Distanzausgleich vorhanden sind.
Antriebssysteme ohne elastische Elemente erwiesen sich bei entsprechender Wartung als ausgesprochen robust und dauerhaft.
Als mit der Ae 4/4 der BLS aber der Siegeszug der laufachslosen Drehgestelle im Lokomotivbau begann, mussten die gewichtigen und entsprechend grossen Antriebe kleineren Baugruppen weichen, welche sich in die spärlichen Platzverhältnisse eines Drehgestelles integrieren lassen.
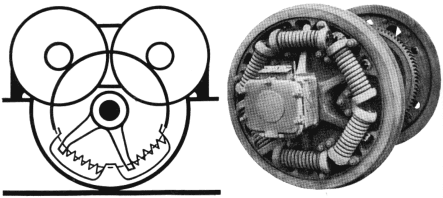
Der Tschanz-Einzelachsantrieb wurde als einer der ersten Einzelachsantriebe entwickelt. Er kam lediglich als Prototyp in zwei Probelokomotiven zur Anwendung.
Das Konzept wurde anschliessend nicht mehr weiter verfolgt, da er in beiden Fällen dem gleichzeitigen entwickelten und ebenfalls im Test befindlichen Buchli-Einzelachsantrieb technisch und wirtschaftlich unterlegen war.
Aufgrund des spärlichen Einsatzes des Tschanz-Antriebes findet er in der gängigen Fachliteratur kaum Beachtung.
Vom fest im Rahmen montierten Fahrmotor (1) wird die Kraft über das Ritzel (2) und ein zweistufiges übersetzungsgetriebe (3) auf eine Kardenwelle übertragen.
Diese Kardanwelle wurde bei beiden Probelokomotiven unterschiedlich ausgeführt:
Während die 1918 umgebaute Be 2/5 über eine lange Kardanwelle verfügte, welche durch die hohle Antriebsachse (4) auf der gegenüberliegende Seite am Triebrad (5) eingriff, verfügte die Ae 4/8 lediglich über je einen kurzen Kardan.
Die Kraftübertragung auf das Triebrad erfolgte somit auf der «Antriebsseite».
Der Tschanz-Einzelachsantrieb konnte aus verschiedenen Gründen nicht überzeugen:
Das zweistufige Getriebe war schwergewichtig, komplex und somit teuer in der Beschaffung und im Unterhalt.
Ebenfalls verursachte es - wie bereits beschrieben - einen gegenüber einstufigen Getrieben schlechteren Wirkungsgrad und fiel durch hohe Lärmemissionen negativ auf.



Der Nachteil von Antriebssystemen mit unelastischen Elementen lag nebst dem hohen Gewicht und der Baugrösse auch im Unterhalt:
Hebel und Kulissen müssen an den Lagerstellen geschmiert werden und sind wegen der Gleitreibung - wenn in diesem Falle auch geringfügig - einem mechanischen Verschleiss unterworfen.
Anfäglich aus rein wirtschaftlichen überlegungen versuchten die Konstrukteure mechanische Ausgleichsmechanismen durch wartungsfreie elastische Elemente zu ersetzen.
Um den kräftemässig hohen Anforderungen im Eisenbahnbau gerecht zu werden, sind für die elastischen Elemente vor allem die metallurgischen Aspekte Voraussetzung für einen störungsfreien Betrieb; waren doch vor allem die Scheiben - und Lamellenantriebe nebst der Torsionsspannung schnell wechselnden Biegebelastungen unterworfen.
Nicht wenige dieser Federelemente gingen unter diesen Bedingungen vorzeitig zu Bruch.